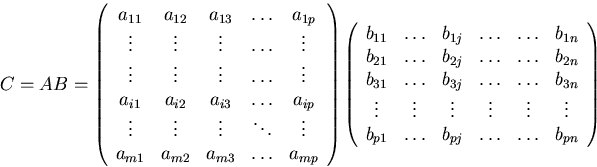
Matrix multiplication is defined in terms of the row-column product:
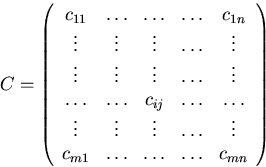
In other words, cij is the dot product of the i-th row-vector of A times the j-th column-vector of B:
, the second row
as 
, etc. Similar, the first column of B is 
,etc.)
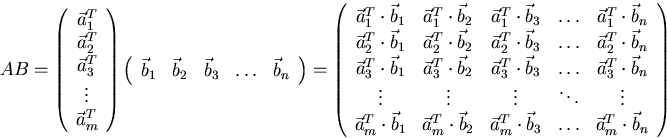
The dots in the above product can be omitted since the matrix product of a row vector times a column vector is by definition the same as the dot product of those vectors.
Multiplication in index notation:
For matrices to be multiplied, the second dimension of A must be the same as the first dimension of B.
Matrix multiplication does not ordinarily commute:
