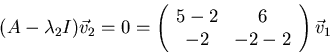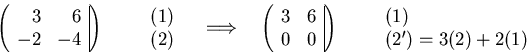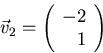Next: 9.47(b), §1 Asked
Up: 9.47
Previous: 9.47(a), §1 Asked
Eigenvalues:
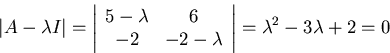
There are two roots: 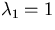 and
and 
The eigenvector corresponding to 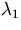 satisfies
satisfies
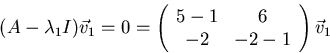
Solving using Gaussian elimination:
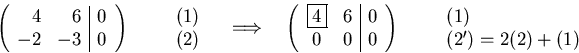
Equation (1) gives 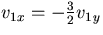 . In order to get a
vector, instead of a set of possible vectors, one component must be
arbitrarily chosen. Remember: undetermined constants in
eigenvectors are not allowed. To get simple numbers, take v1y
= -2, then v1x = 3:
. In order to get a
vector, instead of a set of possible vectors, one component must be
arbitrarily chosen. Remember: undetermined constants in
eigenvectors are not allowed. To get simple numbers, take v1y
= -2, then v1x = 3:
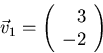
Check:
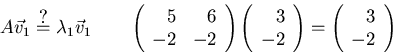
Note: the null space of the matrix above is
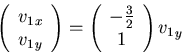
so  would also have been an acceptable eigenvector, just
messier.
would also have been an acceptable eigenvector, just
messier.
The eigenvector corresponding to 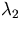 satisfies
satisfies
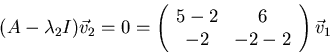
Solving using Gaussian elimination:
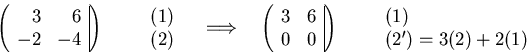
Choosing v2y = 1, then v2x = -2:
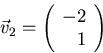
Next: 9.47(b), §1 Asked
Up: 9.47
Previous: 9.47(a), §1 Asked
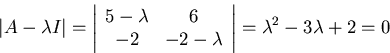
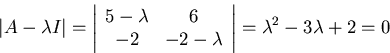
![]() satisfies
satisfies
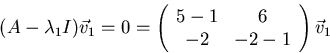
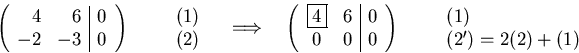
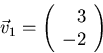
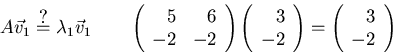
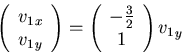
![]() satisfies
satisfies