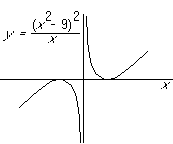p139, #13(a), §3 Alternate

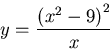
Hence

• intercepts with x-axis are at ;
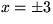• no intercepts with the y axis;
• y is an odd function of x (symmetric about the origin);
• for 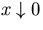, 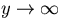(vertical asymptote);
• for 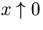, 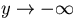(singularity is an odd, simple pole);
• for , .

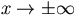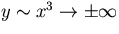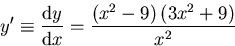
Hence,

• y'>0 for 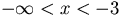(y increases from );
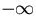• y'=0 for x=-3 (local maximum, y=0);
• y'<0 for -3<x<0 (y decreases towards );
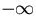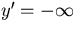• for x=0 (singular point, vertical asymptote);
• y'<0 for 0<x<-3 (decreases from );
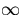• y'=0 for x=3 (local minimum, y=0);
• y'>0 for 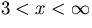(increases to ).

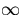Also,

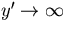• when 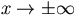(no horizontal or oblique asymptotes);
• all derivatives exist, except at x=0, which has no point on the curve (no corners, cusps, infinite curvature, or other singular points);
• probably no inflection points.

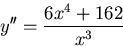
Hence

• really no inflection points (since there is no point at x=0);
• cocave downward for x<0, upward for x>0.

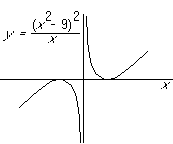
Hence the x- and y-extends as before.